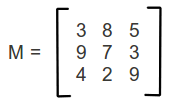Um algoritmo é um conjunto de instruções bem definidas e não ambíguas usadas para resolver problemas, não pode se dizer que é necessariamente um programa, mas o passo a passo para realizar uma tarefa.
Dentro de um algoritmo há diversas estruturas, e duas delas mudam um pouco o conceito de uma simples variável, são chamados de vetores e matrizes.

Vetores

Definição:
É um conjunto de variáveis do mesmo tipo acessíveis com um único nome. Armazenadas de forma contínua e ocupando as posições de forma fixas. Pode-se dizer que vetor é uma matriz unidimensional.

Exemplificando
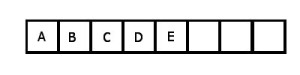
Considere uma sala de aula, onde há 10 alunos e queremos armazenar suas idades em variáveis, até então seria feito assim:

DECLARE idade1, idade2, idade3, idade4, idade5, idade6, idade7, idade8, idade9, idade10 INTEIRO;

Como sabemos, podemos inicializar uma variável de duas formas:
idade1= 10, idade2 = 12, idade3 = 11 … idade10 =10;

Ou pedir que o usuário escreva usando o teclado:

Escreva (“Digite a idade do primeiro aluno”)
Leia (aluno1)
Escreva (“Digite a idade do segundo aluno”)
Leia (aluno2)
…

Não foi tão difícil criar uma variável que armazena a idade de cada aluno, porém, se formos fazer diversos cálculos com as idades ou ainda considerar uma sala com 1000 alunos, já ficaria muito mais difícil. O vetor é uma estrutura que simplifica essas operações com variável do mesmo tipo, considerando que toda idade é do tipo inteiro, criamos um vetor de 10 posições para seguir o mesmo exemplo usado à cima.

idade:vetor[1..10] de inteiro

Na declaração usamos o tamanho máximo que o vetor pode ter, podendo usar o tamanho total declarado ou menos.

Para acessar a idade do primeiro aluno: idade[1]
Para acessar a idade do segundo aluno: idade[2]
…
Para acessar a idade do décimo aluno: idade[10]
idade[1] <- 10=”” br=””> idade[2] <- 11=”” br=””> …
idade[10] <- 10=”” p=””>

Serão armazenadas todas as idades dos respectivos alunos e assim poderão  ser acessadas separadamente. Vem um questionamento: “é quase a mesma dificuldade para acessar em comparação à estrutura simples”. Sim, dessa forma foi, porém será mostrado agora algo bem característico da estrutura vetorial que simplifica as operações com a variável.

São usadas duas variáveis do tipo inteiro para auxiliar na inserção de elementos dentro do vetor. Vou considerar aqui a variável “n” que armazenará o tamanho que meu vetor tiver, e a variável “i” que será usada com o auxilio da estrutura de repetição “para” ou “for” que acessará cada variável de forma mais fácil e rápida como demonstrado à baixo.

algoritmo "vetor"
var
n:inteiro
j:inteiro
valor:inteiro
idade:vetor[1..10] de inteiro

inicio
Escreva("Digite a quantidade de alunos na sala")
Leia(n)

para i de 1 ate n faca
 leia(valor)
 aluno[i] <- valor
fimpara

fimalgoritmo

Usando a variável idade[3] onde i=3, poderemos acessar a idade do 3 aluno, a variável idade[2] onde i=2, acessará a idade do 2 alunos, e assim para todos os outros, assim como já foi demostrado.

Consideramos o fato que precisamos fazer uma média de todos os alunos dentro da sala de aula.
Usando as variáveis de tipo simples e considerando que todas as 10 variável já tenham sido inicializadas com as idades dos respectivos alunos.

DECLARE media NUMERICO; // Essa variável armazenará valores numéricos

media <-  media +(idade1, idade2,idade3, idade4,idade5, idade6, idade7, idade8, idade9, idade10)/10;

Usando vetores

media<- 0; // a variável media precisa ser inicializa com zero
Para i=1; i<=n ; i++ faça // percorrendo todas as idades dos n alunos.
media<- media +idade[i]; // aqui será somente a soma de todas as idades
Fim
media<-media/n ; // aqui será de fato calculado e media.

Como visto até agora, vetores são uma estrutura que simplifica as operações com variáveis do mesmo tipo, trazendo um novo conceito que é bastante usado em quase todos os programas.

Matrizes.

À base da estrutura vetorial, com a diferença de ser n-dimensional, a matrizes tem suas peculiaridades.

Inserção: Assim como o vetor, usamos variáveis auxiliares, porém em matrizes usaremos duas a mais, aqui a variável “LINHAS” armazenará o numero de linhas que a matriz tiver,  a variável “COLUNAS” armazenara a quantidade de colunas que a matriz tiver, e as varialveis “i”e “j” que dentro da estrutura de repetição aqui usada “para” ou “for” para percorrer ou acessar todas as posições.

algoritmo "vetor_matriz"
var
linhas:inteiro
colunas:inteiro
i:inteiro
j:inteiro
valor:inteiro
matriz:vetor[1..3,1..3] de inteiro

inicio

para i de 1 ate 3 faca
escreval("Informe os dados da linha ",i)
para j de 1 ate 3 faca
escreval("Informe os dados da coluna ",j)
leia(valor)
matriz[i,j] <- valor
fimpara
fimpara

i <- 1
j <- 1
para i de 1 ate 3 faca
para j de 1 ate 3 faca
escreva(matriz[i,j])
fimpara
fimpara
fimalgoritmo

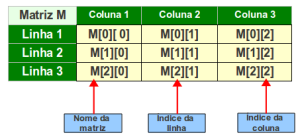
Como mostrado na imagem à cima, todas as pocições possíveis de uma matriz 3×3.

Matrizes também é muito usada para programar jogos.

Neste post foi mostrado de forma simples e básica a estrutura de matrizes e vetores, agora pode-se aplicar esse conceito
à diversas linguagens de programação, busque praticar para fixar o aprendizado.